Skip to main content

Modal Analysis of Fluid Flows: An Overview

Simple aerodynamic configurations under even modest conditions can exhibit complex flows with a wide range of temporal and spatial features. It has become common practice in the analysis of these flows to look for and extract physically important features, or modes, as a first step in the analysis. This step typically starts with a modal decomposition of an experimental or numerical dataset of the flow field, or of an operator relevant to the system. We describe herein some of the dominant techniques for accomplishing these modal decompositions and analyses that have seen a surge of activity in recent decades. For a non-expert, keeping track of recent developments can be daunting, and the intent of this document is to provide an introduction to modal analysis that is accessible to the larger fluid dynamics community. In particular, we present a brief overview of several of the well-established techniques and clearly lay the framework of these methods using familiar linear algebra. The modal analysis techniques covered in this paper include the proper orthogonal decomposition (POD), balanced proper orthogonal decomposition (Balanced POD), dynamic mode decomposition (DMD), Koopman analysis, global linear stability analysis, and resolvent analysis.

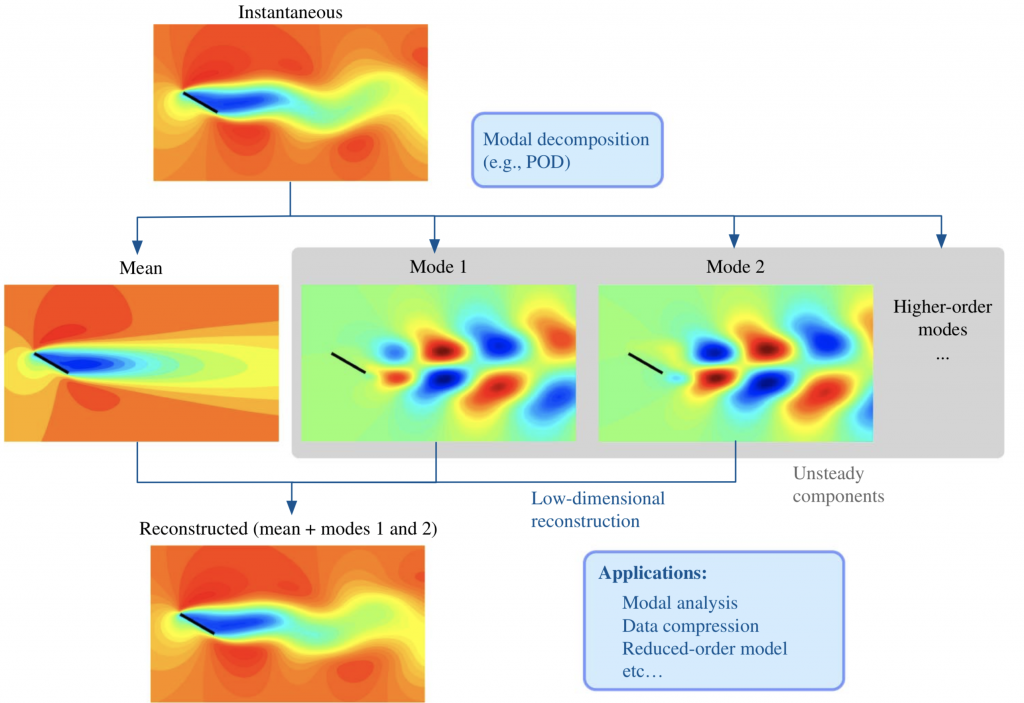
The figure shows the modal decomposition of two-dimensional incompressible flow over a flat-plate wing. This example shows complex nonlinear separated flow being well represented by only two POD modes and the mean flowfield. Visualized are the streamwise velocity profiles.

Literature:

  • [PDF] [DOI] Taira, K., S. L. Brunton, S. Dawson, C. W. Rowley, T. Colonius, B. J. McKeon, O. T. Schmidt, S. Gordeyev, V. Theofilis, and L. S. Ukeiley. “Modal analysis of fluid flows: an overview.” Aiaa journal (2017).
    [Bibtex] 
    @Article{TairaEtAl_2017_AIAAJ,
author = {Taira, K. and Brunton, S. L. and Dawson, S. and Rowley, C. W. and Colonius, T. and McKeon, B. J. and Schmidt, O. T. and Gordeyev, S. and Theofilis, V. and Ukeiley, L. S.},
title = {Modal analysis of fluid flows: An overview},
journal = {AIAA Journal},
year = {2017},
doi = {https://doi.org/10.2514/1.J056060},
file = {:TairaEtAl_2017_AIAAJ.pdf:PDF},
}
Paper, , ,

Spectral Analysis of Jet Turbulence

Informed by LES data and resolvent analysis of the mean flow, we examine the structure of turbulence in jets in the subsonic, transonic, and supersonic regimes. Spectral (frequency-space) proper orthogonal decomposition is used to extract energy spectra and decompose the flow into energy-ranked coherent structures. The educed structures are generally well predicted by the resolvent analysis. Over a range of low frequencies and the first few azimuthal mode numbers, these jets exhibit a low-rank response characterized by Kelvin-Helmholtz (KH) type wavepackets associated with the annular shear layer up to the end of the potential core and that are excited by forcing in the very-near-nozzle shear layer. These modes too the have been experimentally observed before and predicted by quasi-parallel stability theory and other approximations–they comprise a considerable portion of the total turbulent energy. At still lower frequencies, particularly for the axisymmetric mode, and again at high frequencies for all azimuthal wavenumbers, the response is not low rank, but consists of a family of similarly amplified modes. These modes, which are primarily active downstream of the potential core, are associated with the Orr mechanism. They occur also as sub-dominant modes in the range of frequencies dominated by the KH response. Our global analysis helps tie together previous observations based on local spatial stability theory, and explains why quasi-parallel predictions were successful at some frequencies and azimuthal wavenumbers, but failed at others.

The video shows, in quick succession, the raw LES data, a single Fourier component for m=0, and the leading SPOD mode at the same frequency. The streamwise perturbation velocity is visualized.

Literature:

  • [PDF] [DOI] Schmidt, O. T., A. Towne, G. Rigas, T. Colonius, and G. A. Brès. “Spectral analysis of jet turbulence.” Journal of fluid mechanics 855 (2018): 953–982.
    [Bibtex] 
    @Article{SchmidtEtAl_2018_JFM,
author = {Schmidt, O. T. and Towne, A. and Rigas, G. and Colonius, T. and Br{\`e}s, G. A.},
title = {Spectral analysis of jet turbulence},
journal = {Journal of Fluid Mechanics},
year = {2018},
volume = {855},
pages = {953–982},
doi = {10.1017/jfm.2018.675},
file = {:SchmidtEtAl_2018_JFM.pdf:PDF},
publisher = {Cambridge University Press},
}
Paper, , ,

Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis

We consider the frequency domain form of proper orthogonal decomposition (POD) called spectral proper orthogonal decomposition (SPOD). SPOD is derived from a space-time POD problem for stationary flows and leads to modes that each oscillate at a single frequency. We establish a relationship between SPOD and dynamic mode decomposition (DMD); we show that SPOD modes are in fact optimally averaged DMD modes obtained from an ensemble DMD problem for stationary flows. Finally, we establish a connection between SPOD and resolvent analysis. The key observation is that the resolvent-mode expansion coefficients, which are usually treated as deterministic quantities described by an amplitude and phase, should be regarded as statistical quantities, described by their cross-spectral density, in order for the resolvent-mode expansion to properly capture the flow statistics. When the expansion coefficients are uncorrelated, we show that SPOD and resolvent modes are identical.

Literature:

  • [PDF] [DOI] Towne, A., O. T. Schmidt, and T. Colonius. “Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis.” Journal of fluid mechanics 847 (2018): 821–867.
    [Bibtex] 
    @Article{TowneSchmidtColonius_2018_JFM,
author = {Towne, A. and Schmidt, O. T. and Colonius, T.},
title = {Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis},
journal = {Journal of Fluid Mechanics},
year = {2018},
volume = {847},
pages = {821–867},
doi = {10.1017/jfm.2018.283},
file = {:TowneSchmidtColonius_2018_JFM.pdf:PDF},
publisher = {Cambridge University Press},
}
Paper, , ,