Welcome to the Computational Flow Physics Group at UC San Diego! We develop advanced numerical simulation and data-driven analysis tools to understand, model, and predict turbulent and multiphysics flows in engineering and nature. Our work combines high-fidelity computation with modal decomposition and feature extraction to reveal coherent flow structures and translate them into predictive reduced-order models for forecasting and optimization. We focus on aerospace problems, including jet noise control, unsteady aerodynamics and aeroacoustics, transition, dynamic stall, aero-optics, and hypersonics. While our work is grounded in physics-based modeling, we also curiously explore where modern machine learning can complement first-principles simulation, statistical methods, and classical closure techniques. Beyond aerospace, our methods extend to complex geophysical flows, with applications in atmospheric science and physical oceanography.
News
| Dec 19, 2025 |
Forecasting how real-world flows evolve is notoriously challenging. Take a look at our new article (Schmidt, 2026) on Space–Time Projection for forecasting high-dimensional transient and stationary flows.

|
| Dec 11, 2025 |
Computational Flow Physics Group annual holiday dinner—2025 edition!

|
| Dec 01, 2025 |
Congratulations to Cong Lin on our CMAME paper (Frame et al., 2025), and many thanks to Peter Frame and Aaron Towne for a fantastic collaboration with two outstanding researchers. We also highly recommend Peter and Aaron’s extension of the framework to fully nonlinear models (arXiv:2411.13531).

|
| Oct 01, 2025 |
Congratulations to Tianyi Chu on our Proceedings of the Royal Society A paper (Chu & Schmidt, 2025) on stochastic reduced-order Koopman modeling for turbulent flows.
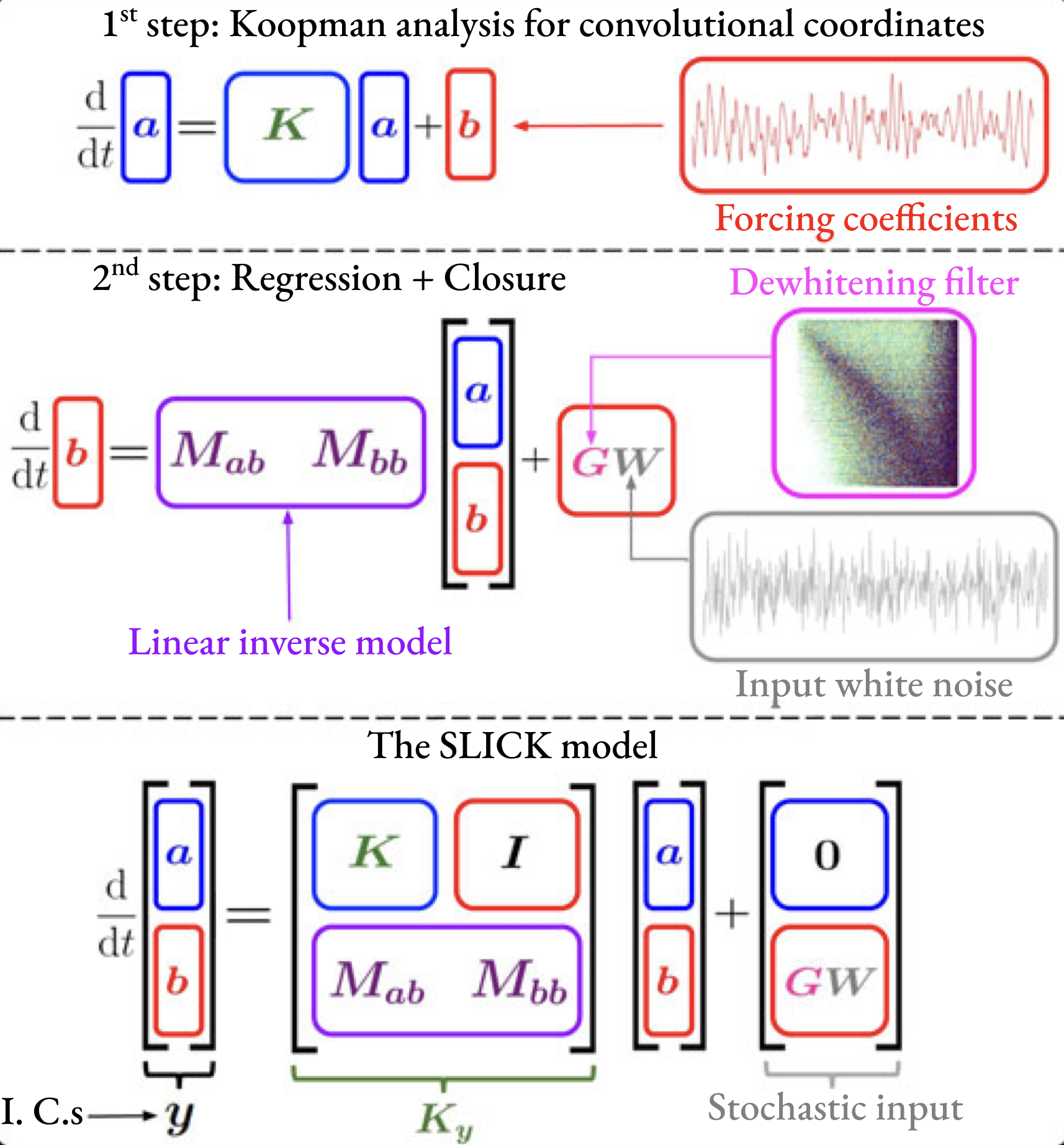
To put our method into perspective within the zoo of data-driven and operator-based approaches, Tianyi's figure below provides an overview of basis-identification strategies for model order reduction:

|
| Sep 17, 2025 |
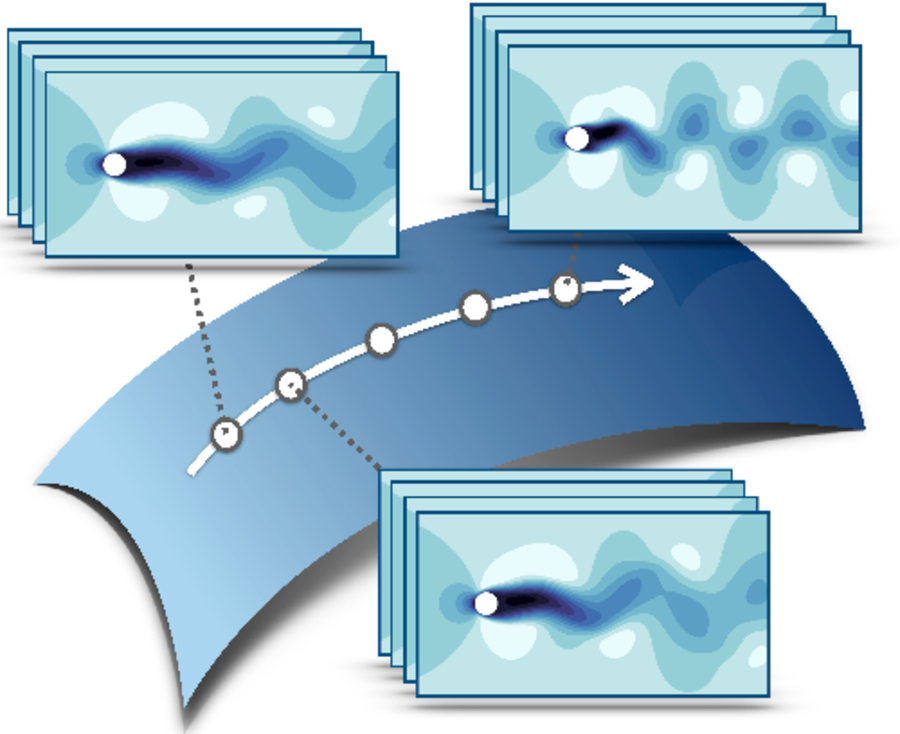
Happy to share our JFM paper (Sato & Schmidt, 2025) on parametric reduced-order modeling and mode sensitivity—huge thanks and congratulations to my colleague Shintaro Sato for leading this work.
|
| Sep 04, 2025 |
Excited to share our JFM paper (Nekkanti et al., 2025) on time-delay modeling and coherent-structure dynamics in jets—thank you Akhil Nekkanti and Tim Colonius; it's always a pleasure collaborating!

|
| Sep 02, 2025 |
Big congratulations to Brandon Yeung for the great work on our JFM paper (Yeung & Schmidt, 2025) exploring spectral dynamics of natural and forced supersonic twin-rectangular jets.

|
| May 19, 2025 |
Schmid happens! Hosting Peter Schmid during his Penner Lecture visit.

|
| Feb 01, 2025 |
Our CPC paper on Robust SPOD (Colanera et al., 2025) is out—many thanks to our collaborators Antonio Colanera and Matteo Chiatto from the University of Naples Federico II.

|
-
Stochastic reduced-order Koopman model for turbulent flows
T.
Chu, and O. T.
Schmidt
Proceedings of the Royal Society A, 2025, 481(2323), 20250270
A stochastic data-driven reduced-order model applicable to a wide range of turbulent natural and engineering flows is presented. Combining ideas from Koopman theory and spectral model order reduction, the stochastic low-dimensional inflated convolutional Koopman model accurately forecasts short-time transient dynamics while preserving long-term statistical properties. A discrete Koopman operator is used to evolve convolutional coordinates that govern the temporal dynamics of spectral orthogonal modes, which, in turn, represent the energetically most salient large-scale coherent flow structures. Turbulence closure is achieved in two steps: first, by inflating the convolutional coordinates to incorporate nonlinear interactions between different scales, and second, by modelling the residual error as a stochastic source. An empirical dewhitening filter informed by the data is used to maintain the second-order flow statistics. The model uncertainty is quantified through either Monte–Carlo simulation or by directly propagating the model covariance matrix. The model is demonstrated on the Ginzburg–Landau equations, large-eddy simulation data of a turbulent jet, and particle image velocimetry data of the flow over an open cavity. In all cases, the model is predictive over time horizons indicated by a detailed error analysis and integrates stably over arbitrary time horizons, generating realistic surrogate data.
-
Parametric reduced-order modelling and mode sensitivity of actuated cylinder flow from a matrix manifold perspective
S.
Sato, and O. T.
Schmidt
Journal of Fluid Mechanics, 2025, 1021, A44
-
Spectral dynamics of natural and forced supersonic twin-rectangular jet flow
B.
Yeung, and O. T.
Schmidt
Journal of Fluid Mechanics, 2025, 1018, A34
-
Nonlinear dynamics of vortex pairing in transitional jets
A.
Nekkanti, T.
Colonius, and O. T.
Schmidt
Journal of Fluid Mechanics, 2025, 1018, A32
-
Linear model reduction using spectral proper orthogonal decomposition
P.
Frame, C.
Lin, O. T.
Schmidt, and
1 more author
Computer Methods in Applied Mechanics and Engineering, 2025, 447, 118382
Most model reduction methods reduce the state dimension and then temporally evolve a set of coefficients that encode the state in the reduced representation. In this paper, we instead employ an efficient representation of the entire trajectory of the state over some time interval of interest and then solve for the static coefficients that encode the trajectory on the interval. We use spectral proper orthogonal decomposition (SPOD) modes, which are provably optimal for representing long trajectories and substantially outperform any representation of the trajectory in a purely spatial basis (e.g., POD). We develop a method to solve for the SPOD coefficients that encode the trajectories for forced linear dynamical systems given the forcing and initial condition, thereby obtaining the accurate prediction of the dynamics afforded by the SPOD representation of the trajectory. The method, which we refer to as spectral solution operator projection (SSOP), is derived by projecting the general time-domain solution for a linear time-invariant system onto the SPOD modes. We demonstrate the new method using two examples: a linearized Ginzburg-Landau equation and an advection-diffusion problem. In both cases, the error of the proposed method is orders of magnitude lower than that of POD-Galerkin projection and balanced truncation. The method is also fast, with CPU time comparable to or lower than both benchmarks in our examples. Finally, we describe a data-free space-time method that is a derivative of the proposed method and show that it is also more accurate than balanced truncation in most cases.
-
Robust spectral proper orthogonal decomposition
A.
Colanera, O. T.
Schmidt, and M.
Chiatto
Computer Physics Communications, 2025, 307, 109432
Experimental measurements often present corrupted data and outliers that can strongly affect the main coherent structures extracted with the classical modal analysis techniques. This effect is amplified at high frequencies, whose corresponding modes are more susceptible to contamination from measurement noise and uncertainties. Such limitations are overcome by a novel approach proposed here, the robust spectral proper orthogonal decomposition (robust SPOD), which implements the robust principal component analysis within the SPOD technique. The new technique is firstly presented with details on its algorithm, and its effectiveness is tested on two different fluid dynamics problems: the subsonic jet flow field numerically simulated, and the flow within an open cavity experimentally analyzed in [48]. The analysis of the turbulent jet data, corrupted both with salt and pepper and Gaussian noise, shows how the robust SPOD produces more converged and physically interpretable modes than the classical SPOD; moreover, the use of the robust SPOD as a tool for de-noising data, based on the signal reconstruction from de-noised modes, is also presented. Applying robust SPOD to the open cavity flow has revealed that it yields smoother spatial distributions of modes, particularly at high frequencies and when considering higher-order modes, compared to standard SPOD.
-
Data-driven forecasting of high-dimensional transient and stationary processes via space–time projection
O. T.
Schmidt
Proceedings of the Royal Society A, 2026, 482, 20250454
Support & Acknowledgments
We are grateful for the support of the U.S. National Science Foundation, the U.S. Department of Energy, the U.S. Air Force Office of Scientific Research,the U.S. Office of Naval Research, the U.S. Army Research Office, and the NISEC and ACCORD centers. We sincerely thank the program officers and center leadership for their sustained commitment to fundamental research and its translation to impactful applications.
















